АВТОКОРРЕЛЯЦИЯ В ОСТАТКАХ. КРИТЕРИЙ ДАРБИНА-УОТСОНА.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF
В данной статье пойдет речь о временных рядах в эконометрике, мы раскроем тему: "Автокорреляция в остатках. Критерий Дарбина-Уотсона."
Информационной базой для анализа экономических процессов являются динамические и временные ряды. Совокупность наблюдений некоторого явления, упорядоченная в зависимости от последовательности значений другого явления называют динамическим рядом. Динамические ряды, у которых в качестве признака упорядочения используется время, называют временными.
Временной ряд - это набор чисел, привязанный к последовательным, обычно равноотстоящим моментам времени. Числа, составляющие временной ряд и получающиеся в результате наблюдения за ходом некоторого процесса, называются уровнями временного ряда или элементами. Под длиной временного ряда понимают количество входящих в него уровней n. Временной ряд обычно обозначают Y(t), или ![]() , где t=1,2,...,n.
, где t=1,2,...,n.
В общем случае каждый уровень временного можно представить как функцию четырех компонент: f(t), S(t), U(t), (t) , отражающих закономерность и случайность развития.
Где f(t) - тренд (долговременная тенденция) развития; S(t) - сезонная компонента; U(t) -циклическая компонента; (t)- остаточная компонента.
Важнейшей классической задачей при исследовании экономических временных рядов является выявление и статистическая оценка основной тенденции развития изучаемого процесса и отклонений от нее.
Автокорреляция в остатках может быть вызвана несколькими причинами, имеющими различную природу.
- Она может быть связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака.
- В ряде случаев автокорреляция может быть следствием неправильной спецификации модели.
От истинной автокорреляции остатков следует отличать ситуации, когда причина автокорреляции заключается в неправильной спецификации функциональной формы модели. В этом случае следует изменить форму модели, а не использовать специальные методы расчета параметров уравнения регрессии при наличии автокорреляции в остатках.
Существует два наиболее распространенных метода определения автокорреляции остатков:
- Построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции.
- Использование критерия Дарбина - Уотсона и расчет величины.
Критерий Дарбина-Уотсона (или DW-критерий) - статистический критерий, используемый для тестирования автокорреляции первого порядка элементов исследуемой последовательности. Наиболее часто применяется при анализе временных рядов и остатков регрессионных моделей.
Критерий назван в честь Джеймса Дарбина и Джеффри Уотсона. Критерий Дарбина-Уотсона рассчитывается по следующей формуле:
где ![]() - коэффициент автокорреляции первого порядка.
- коэффициент автокорреляции первого порядка.
Eсли в остатках существует полная положительная автокорреляция и , то . Если в остатках полная отрицательная автокорреляция, то и, следовательно, . Если автокорреляция остатков отсутствует, то и . Т.е. .
На практике применение критерия Дарбина-Уотсона основано на сравнении величины ![]() с теоретическими значениями
с теоретическими значениями ![]() и
и ![]() для заданного числа наблюдений
для заданного числа наблюдений ![]() , числа независимых переменных модели
, числа независимых переменных модели ![]() и уровня значимости
и уровня значимости ![]() .
.
-
- Если
 , то гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция);
, то гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция); - Если
 , то гипотеза не отвергается;
, то гипотеза не отвергается; - Если
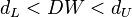 , то нет достаточных оснований для принятия решений.
, то нет достаточных оснований для принятия решений.
- Если
Когда расчётное значение ![]() превышает 2, то с
превышает 2, то с ![]() и
и ![]() сравнивается не сам коэффициент
сравнивается не сам коэффициент ![]() , а выражение
, а выражение ![]() .
.
Также с помощью данного критерия выявляют наличие коинтеграции между двумя временными рядами. В этом случае проверяют гипотезу о том, что фактическое значение критерия равно нулю. С помощью метода Монте-Карло были получены критические значения для заданных уровней значимости. В случае, если фактическое значение критерия Дарбина-Уотсона превышает критическое, то нулевую гипотезу об отсутствии коинтеграции отвергают.
Существует несколько недостатков критерия Дарбина -Уотсона, таких как:
-
- Неприменимость к моделям авторегрессии, а также к моделям с гетероскедастичностью условной дисперсии и GARCH-моделям.
- Неспособность выявлять автокорреляцию второго и более высоких порядков.
- Даёт достоверные результаты только для больших выборок.
- Не подходит для моделей без свободного члена (для них статистика, аналогичная
 , была рассчитана Fairbrother).
, была рассчитана Fairbrother). - Дисперсия коэффициентов будет расти, если
 имеет распределение, отличающееся от нормального.
имеет распределение, отличающееся от нормального.
Критерий Дарбина-Уотсона неприменим для моделей авторегрессии, так как он для подобного рода моделей может принимать значение, близкое к двум, даже при наличии автокорелляции в остатках. Для этих целей используется ![]() -критерий Дарбина.
-критерий Дарбина.
![]() -статистика Дарбина применима тогда, когда среди объясняющих регрессоров есть
-статистика Дарбина применима тогда, когда среди объясняющих регрессоров есть ![]() . На первом шаге методом МНК строится регрессия. Затем критерий
. На первом шаге методом МНК строится регрессия. Затем критерий ![]() Дарбина применяется для выявления автокорреляции остатков в модели с распределёнными лагами:
Дарбина применяется для выявления автокорреляции остатков в модели с распределёнными лагами:
![]()
где
 - число наблюдений в модели;
- число наблюдений в модели; - оценка дисперсии коэффициента при лаговой результативной переменной
- оценка дисперсии коэффициента при лаговой результативной переменной  .
.
Для панельных данных используется немного видоизменённый критерий Дарбина-Уотсона:

В отличие от критерия Дарбина-Уотсона для временных рядов, в этом случае область неопределенности является очень узкой, в особенности для панелей с большим количеством индивидуумов.
В ходе изучения последовательности остатков временного ряда в такой дисциплине как эконометрика, можно построить график их зависимости от времени. В соответствии с предпосылками метода наименьших квадратов, остатки должны быть случайными (а). Однако, в процессе моделирования временных рядов иногда встречается такая ситуация, когда остатки содержат тенденцию (б и в) или циклические колебания (г). Из этого можно сделать вывод, что каждое следующее значение зависит от предыдущих.
Рассмотрим пример модели зависимости остатков времени на графике:
Модели зависимости остатков от времени
а- случайные остатки; б - возрастающая тенденция в остатках; в - убывающая тенденция в остатках; г - циклические колебания в остатках
В процессе выявления автокорреляции остатков по критерию Дарбина - Уотсона выдвигается гипотеза об ее отсутствии. Альтернативные гипотезы о наличии положительной или отрицательной автокорреляции в остатках. После чего по таблицам определяются критические значения критерия Дарбина - Уотсона dL и du для заданного числа наблюдений и числа независимых переменных модели при уровне значимости а (обычно 0,95). По этим значениям промежуток {0;4} разбивают на пяти отрезков:
Если расчетное значение критерия Дарбина - Уотсона попадает в зону неопределенности, то подтверждается существование автокорреляции остатков и гипотезу отклоняют.
Рассмотрим пример:
Определим наличие автокорреляции с помощью критерия Дарбина - Уотсона:
|
Номер |
ei |
ei - еi-1 |
(ei - еi-1)2 |
|
|
8,3 |
|
|
|
|
4,26 |
-4,04 |
16,32 |
|
|
-12,46 |
-16,72 |
279,56 |
|
|
-1,86 |
10,6 |
112,36 |
|
|
-7,38 |
-5,52 |
30,47 |
|
|
5,26 |
12,64 |
159,77 |
|
|
-9,66 |
-14,92 |
222,61 |
|
|
-2,26 |
7,4 |
54,76 |
|
|
8,34 |
10,6 |
112,36 |
|
|
7,46 |
-0,88 |
0,77 |
|
Сумма |
|
|
988,98 |
1.Заполняем таблицу. Из каждого числа 2-го столбца вычитаем предыдущее число. 2-го столбца и результат пишем в 3-м столбце. В 4-м столбце числа округляем до двух знаков после запятой.
2.По таблице распределения Дарбина-Уотсона находим dl = 0,697 и du = 1,641. Тогда 4 - du = 4 - 1,641 = 2,359.
3.Так как du < DW < 4 - du (1,641 < 1,793 < 2,359), то гипотеза об отсутствии автокорреляции остатков не отклоняется на уровне значимости 0,05. Это является одним из подтверждений высокого качества модели.
Следуя из всего выше изложенного, следует то, что критерий Дарбина-Уотсона используется для обнаружения автокорреляции остатков модели регрессии автокорреляционной и частной автокорреляционной функции. Однако данный критерий можно применять только для обнаружения автокорреляции первого порядка между соседними рядами случайных остатков.
